2.3 Special mathematical expectations (특별한 수학적 기댓값)
2.3 Special mathematical expectations (특별한 수학적 기댓값)

- 분산은 mu에 대한 2차 적률의 결과이다.
- 평균에 대한 1차 적률은 0이다. (계산해보면 나옴)
Definition 4. Mement generating function (적률생성함수)

표본공간이 S이고 확률질량함수 f(x)를 갖는 이산형의 확률변수를 X라고 하자. 유한한 -h < t < h (h는 양수)에 대해

가 존재하면

M(t) = E(e^tX)를 X의 적률생성함수 mgf라고 한다.
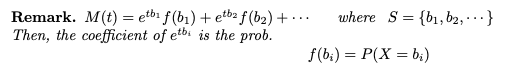
e^tb_i의 계수인 f(b_i)는 확률함수이다.
즉 위의 상황에서 S = {b_1, b_2, ..., b_n} 일 것이다.
Uniqueness of moment generating function(mgf) 적률생성함수의 유일성

두 확률변수가 같은 mgf를 갖는다면, 반드시 같은 확률분포를 갖는다.
두 확률변수가 f(x), g(y) 두 개 확률질량함수와 같은 sample space {b_1,b_2, ...}를 갖는다면, 모든 t에 대해서 위와 같은 적률생성함수를 갖기 때문이다.
즉, 그럼 수학적 변환 이론에 따라 다음의 식이 인정된다.

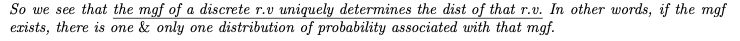
우리는 무작위 확률변수의 분포를 이산형 확률 변수의 적률생성함수가 유일하게 결정한다는 것을 알고 있다.
Ex 2.3-7
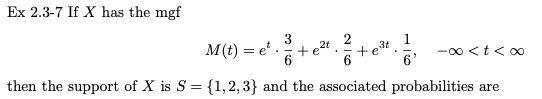
X가 위와 같은 mgf(적률생성함수)를 갖는다면 X의 support(정의역)는 S = {1, 2, 3}이며 관련된 확률은 다음과 같다.


또한 X가 확률질량함수를 가진다는 전제하에 다음과 같이 확률함수를 쓸 수있다.
Ex 2.3-8
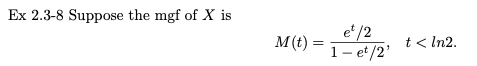
X의 적률생성함수가 다음과 같다고 가정해보자.
이 적률생성함수를 가지고 바로 확률변수 X의 확률질량함수를 떠올리기는 쉽지 않다.

과거에 배운 테일러 전개를 생각해보자. 이걸 통해


X의 다음과 같은 확률질량함수를 알 수 있다.


라플라스 변환이론으로부터 M(t)가 t = 0에서 연속임을 알 수 있다. 또한 수열이 균일 수렴할 때 미분과 summation은 교환 가능하다.

Ex 2.3-9

X가 예제 2.2-6의 기하분포를 갖는다고 가정하자. 그럼 X의 확률질량함수는 위와 같다.
그럼 X의 적률생성함수는?

