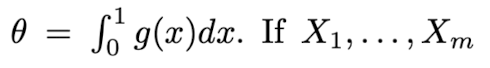
임의의 함수 g(x)에 대해서 [0,1]구간의 적분한 값을 theta로 하여 추정하는 문제를 생각해보자.
여기서 X는 U(0,1)에서 추출된 샘플이다.

theta가 g(x)의 평균이라 할때, 대수의 법칙에 의해서 theta를

으로 추정할 수 있게된다.
monte carlo method는 과정을 이용한다.

이 친구를 계산해보자. 접근법이 두가지가 있지만 난 첫번째가 아닌 두번째 접근법을 사용하겠다. 왜냐하면 교수님께서 두 번째 접근법이 더 확장성이 좋다고 하셨음.
X~ U(a,b)라고 하고, 우리는 위의 식을 아래와 같이 변환할 수 있다. (b-a)/(b-a) = 1 이므로.
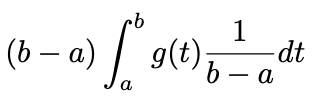
근데 1/b-a 은 균일분포의 pdf이고 같은 구간에서 적분한 값은 1이 된다.
때문에 (b-a)Ex~U(0,1)[g(x)]라는 결론이 나온다.
