Definition 1.3.1

B사건이 발생했다는 전제 하에 A사건에 대한 조건부확률의 정의는 다음과 같다.
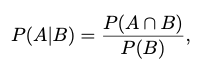
provided that P(B) > 0.
물론 B가 일어날 확률은 0보다 커야만 한다.

실험의 결과에 B가 속한다 한다면, A의 확률은 얼마인가?
우리는 효과적으로 표본공간을 B로 제한하고 있다.


4면의 공정한 주사위 한 쌍을 굴려서 그 합을 결정한다. A를 합이 3인 사건이라하고, B를 합이 3 또는 5가 나온 것으로 하자. 연속으로 굴렸을 때, 합이 5가 나오기 전에 3이 나올 확률은 조건부확률로 생각할 수 있다.
3 혹은 5라는 합이 발생했다고 전제하고 3이 합으로 나올 확률. 바로 조건부확률이다.
B 전제 하에 A의 조건부확률은 다음과 같다.

Ex 1.3-5

공정한 게임에서 보드위에 풍선 25개가 있는데, 10개는 노랑, 8개는 빨강, 7개는 초록이다. A 선수는 상을 받기 위해 풍선으로 다트를 던지고 무작위로 그것 중 하나를 맞춘다. 첫 번째로 맞춘 풍선이 노랑이라고 했을 때, 그 다음 풍선 또한 노랑일 확률은 얼마인가?
24개의 남은 풍선 중 0개는 노랑일 것이고, 조건부확률은 대입한 자연스러운 값은 9/24이다.
Definition 1.3.2 the multiplication rule 곱셈 규칙

두 개의 사건 A, B가 같이 발생할 확률은 곱셈 규칙이 적용된다.


A그릇에는 7개의 파란 칩과, 3개의 빨간 칩이 있다. 두 개의 칩이 연속적으로 무작위로 비복원 추출된다.
우리는 그 확률은 계산하고 싶다. 첫 번째 뽑기의 결과가 빨간 칩(A), 두 번째 뽑기의 결과가 파란 칩(B).
여기엔 다음과 같은 확률을 할당하는 것이 합리적이다.

빨간칩을 뽑을 확률은 10개중에 3개가 있으므로 P(A) = 3/19, 첫 번째에 빨간 칩을 뽑고 파란 칩을 뽑을 확률은 9개중 7개가 존재하는 파란칩을 뽑을 확률이므로 7/9

즉. 첫 번째 뽑기에 빨간 것을 얻고, 두 번째에 파란 것을 뽑을 확률은 다음과 같다.

- Extension of multiplication rule 곱셉 규칙의 확장

Ex 1.3-10

A 초등학교 학생은 5개의 파란색 구슬, 4개의 하얀색 구슬을 왼쪽 주머니에 가지고 있고, 4개의 파란색 구슬, 5개의 하얀색 구슬을 오른쪽 주머니에 가지고 있다. 만약 학생이 구슬 한 개를 무작위로 왼쪽 주머니에서 오른쪽 주머니로 옮긴다면, 오른쪽 주머니로부터 파란 구슬을 뽑을 확률은 얼마인가?
표기를 위해 BL은 왼쪽 주머니에서 파란 구슬, BR은 오른쪽 주머니에서 파란 구슬, WL은 왼쪽 주머니에서 하얀 구슬을 뽑은 것이라 하자.

'studies > 수리통계학1' 카테고리의 다른 글
| 2.1 Discret distributions 이산형 분포 (0) | 2023.03.29 |
|---|---|
| 1.5 Bayes' Theorem. 베이지안 정리 (0) | 2023.03.12 |
| 1.4 Independent events. 독립 사건 (1) | 2023.03.12 |
| 1.2 Methods of enumerataion (나열 방법) (2) | 2023.03.12 |
| 1.1 Properties of Probability & four definitions 확률의 속성과 네 가지 정의. (1) | 2023.03.11 |
