2.4 The Binomial Dist. (이항 분포)
Definition 5. A Bernoulli experiment (베르누이 시행)

베르누이 시행은 무작위 실험으로, 그 결과는 상호 배타적이고 완전하게 성공 혹은 실패로 분류할 수 있다.
Definition 6. A sequence of Bernoulli trials (연속된 베르누이 시행)

연속된 베르누이 시행는 베르누이 시행이 여러번 독립적으로 수행됐을 때 발생한다. 성공에 대한 확률은 매 시행마다 같게 유지된다.
Ex 2.4-1

사탕무 씨앗의 발아율은 0.8이고 씨앗의 발아는 성공이라고 표현하겠다. 10개의 씨앗을 심고 한 씨앗의 발아가 독립적이라고 가정했을 때, 또다른 씨앗의 발아율은 확률 p가 0.8인 10번의 베르누이 시행과 동일할 것이다.
Definition 7. Bernoulli dist (베르누이 분포)

다음의 정의의 베르누이 시행과 관련된 무작위 확률 변수를 X라 하자.


그럼 X의 확률질량함수는 다음과 같다. 그리고 우리는 이 X가 베르누이 분포를 갖는다고 할 수 있다.
Ex 2.4-4

beet seed 5개가 row에 심어졌다고 했을 때, 관측 가능한 순서는 (1,0,1,0,1)로 1,3,5번째는 발아했고 나머지 둘은 죽었다. 만약 발아 성공율이 0.8이고 확률들이 독립적이라는 가정하에 결과가 나타날 수 있는 확률은 다음과 같다.

Definition 8. Binomial dist (이항분포)

일련의 베르누이 시행에서 그것이 발생한 실제 순서가 아닌 전체 성공 횟수를 X라 하자.
각 시행들은 독립적이고, 성공과 실패의 확률은 각각 p, q=1-p이므로 이 사건의 확률은 위와 같을 것이다. 그럼 우리는 이러한 사건의 확률함수를 다음과 같이 나타낼 수 있고 이러한 X가 이항분포를 갖는다고 말한다.

n번의 시행 중 x가 언제 발생하는지는 중요하지 않기 때문에 combination을 베르누이 시행 앞에 추가해주는 것이 포인트다.

Ex 2.4-5

당첨이 20%인 즉석복권에서 X가 n번의 구매에서 당첨될 숫자라고 하자. 두 개의 당첨 복권을 구매할 확률은 다음과 같다.

Ex 2.4-7

10번의 독립시행에서 발아한 씨앗의 숫자를 X라고하고 하면 이 시행은 시행 횟수 10 성공 확률 0.8인 이항분포이다. 그럼 확률함수는 다음과 같다.
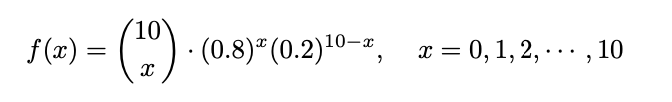

P(X<=8)은 P(Y>=2) 씨앗이 2개 이하로 발아에 실패할 확률과 같다.

Remark. mgf of Binomial distribution (이항분포의 적률생성함수)


Remark. Mean and variance of Bin(n,p)

'studies > 수리통계학1' 카테고리의 다른 글
| 2.6 The Negative Binomial Dist 음이항 분포 (0) | 2023.03.29 |
|---|---|
| 2.5 The Hypergeometric Dist. (초기하분포) (0) | 2023.03.29 |
| 2.3 Special mathematical expectations (특별한 수학적 기댓값) (0) | 2023.03.29 |
| 2.1 Discret distributions 이산형 분포 (0) | 2023.03.29 |
| 1.5 Bayes' Theorem. 베이지안 정리 (0) | 2023.03.12 |
